pwnable.kr - collision

Recommended Reading

• Hash Collision
• Checksum
• Symbolic Execution
• Satisfiability Modulo Theories

Write-up

The collision challenge is the second of the Toddler’s Bottle challenges in pwnable.kr. Although this is a very simple challenge, we’ll show 3 different ways to solve it, from a simple algebraic method to more complex symbolic execution and SMT solvers. The description of the challenge is the following:

Daddy told me about cool MD5 hash collision today. I wanna do something like that too!

ssh [email protected] -p2222 (pw:guest)

As per the previous challenge, we can log into the server and check we’re in the /home/col directory with the following:

col@pwnable:~$ ls -lah
total 36K
drwxr-x---   5 root    col     4.0K Oct 23  2016 .
drwxr-xr-x 116 root    root    4.0K Nov 11  2021 ..
d---------   2 root    root    4.0K Jun 12  2014 .bash_history
-r-sr-x---   1 col_pwn col     7.2K Jun 11  2014 col
-rw-r--r--   1 root    root     555 Jun 12  2014 col.c
-r--r-----   1 col_pwn col_pwn   52 Jun 11  2014 flag
dr-xr-xr-x   2 root    root    4.0K Aug 20  2014 .irssi
drwxr-xr-x   2 root    root    4.0K Oct 23  2016 .pwntools-cache

Knowing the conditions to access the flag, let’s jump directly to the contents of the col.c file:

 1#include <stdio.h>
 2#include <string.h>
 3unsigned long hashcode = 0x21DD09EC;
 4unsigned long check_password(const char* p){
 5    int* ip = (int*)p;
 6    int i;
 7    int res=0;
 8    for(i=0; i<5; i++){
 9        res += ip[i];
10    }
11    return res;
12}
13
14int main(int argc, char* argv[]){
15    if(argc<2){
16        printf("usage : %s [passcode]\n", argv[0]);
17        return 0;
18    }
19    if(strlen(argv[1]) != 20){
20        printf("passcode length should be 20 bytes\n");
21        return 0;
22    }
23
24    if(hashcode == check_password( argv[1] )){
25        system("/bin/cat flag");
26        return 0;
27    }
28    else
29        printf("wrong passcode.\n");
30    return 0;
31}

We must reach line 25 to make the program print the contents of the flag file. Let’s backtrace from there and understand what constraints we must meet:

• In line 24 the return of check_password(argv[1]) must match 0x21DD09EC
• In line 19 argv[1] must have 20 bytes (chars)

Let’s now focus on the check_password function, we control it’s input and want to make the output match 0x21DD09EC:

 1unsigned long hashcode = 0x21DD09EC;
 2unsigned long check_password(const char* p){
 3    int* ip = (int*)p;
 4    int i;
 5    int res=0;
 6    for(i=0; i<5; i++){
 7        res += ip[i];
 8    }
 9    return res;
10}

The function converts our input (char *) into an int *, we know that our input is 20 bytes, and each int is 4 bytes long, so our input becomes an int array of size 5. It then iterates that array, summing each position into the res variable, which is then returned, and consequently checked against the hashcode value.

In sum, this function is very similar to a Sum Complement checksum: it creates an int array from the argument, and returns the sum of all the elements of the array.

Let’s now explore different ways to solve this.

Algebraic method

The first and simplest way to solve this is to use basic algebra. Knowing that the sum of the 5 chunks must be equal to 568134124 (0x21DD09EC) we can do an integer division by 5:

568134124 / 5 = 113626824

If 568134124 was divisible by 5, we’d be done, but since it isn’t we must check how off we are from the hashcode value. The closest and lower divisible by 5 number would be 568134120, so we’re off by 4:

568134124 - 113626824 * 5 = 4

Our chunks should then be:

113626824 113626824 113626824 113626824 113626828
or in hex:
0x06C5CEC8 0x06C5CEC8 0x06C5CEC8 0x06C5CEC8 0x06C5CECC

Finally, we should check that there are no null bytes, which there aren’t. This is relevant because the argv would break at the null byte and consider the remaining as another argument.

Our final payload should take into consideration that we are sending a char * that gets interpreted as an int *, so we must flip the endianness when the send the values, hence the the payload is (in hex):

C8CEC506C8CEC506C8CEC506C8CEC506CCCEC506

We must now send this payload as an argument to the col binary. We’ll leave this as an exercise for the reader. :)

angr method

The second method serves to showcase the angr framework. This allows us to do symbolic execution on our binary, which enables us to find what inputs will provide a specific output. In our col binary, this would mean finding the string that would return the hashcode we need.

Symbolic execution in angr is done by creating an abstract syntax tree (AST) which is converted into constraints that are fed to a satisfiability modulo theories (SMT) solver. The SMT solver will check if our constraints are satisfiable (i.e. solvable) and provide an input that is valid for the constraints.

All of this symbolic execution stuff may seem complex (we’ll go into more detail in the z3 method section), but angr abstracts all of this for us.

To use angr we just need to know some basic concepts:

• Binary files are loaded into a Project object, from where we can create other objects specific to our binary.
• To represent the binary at a specific point in time we use a program state. This represents the state of the memory, registers, etc. These states make use of concrete and symbolic values to represent the state of the program.
• To add specific constraints to the state (e.g. byte at position 0x100 must be bigger than 0x10) we use BitVector Symbols (BVS) for symbolic values, or BitVector Values (BVV) for concrete values.
• To do symbolic execution we need a simulation manager. This will take a state and move it around in time (e.g. step forward).

For our specific case, we need to reverse and binary and find where we want our program state to start. We could simply tell it to start from the entrypoint (i.e. main), but this would increase the complexity of the symbolic execution, making it slower or not even runnable.

Below is an image that shows the relevant part we want to symbolically execute.

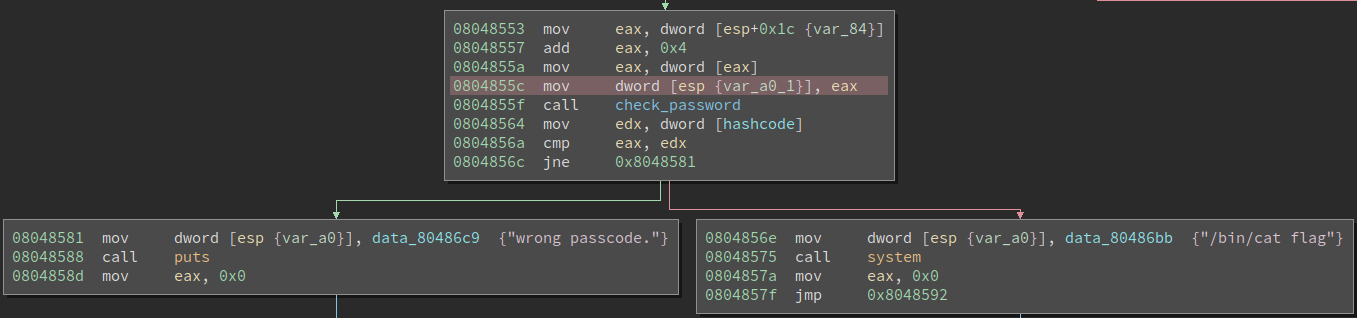
In red is the address where we want to start our execution: 0x804855c. The block on the right is what we want to hit, starting at address 0x804856e. The block on the left is what we want to avoid, starting at address 0x8048581. Furthermore, we must note that the check_password function receives its arguments via the stack (address in red).

Using all this information we can now create a script to find our magic input string:

 1import angr
 2import claripy
 3
 4def main():
 5    project = angr.Project('./col')
 6
 7    # The addresses that are relevant for the execution
 8    start_addr = 0x804855c
 9    good_addr = 0x804856e
10    bad_addr = 0x8048581
11    pass_addr = 0x80000000
12
13    # We use a blank_state, which is the program in a... blank state,
14    # nothing is set. The options we set will fill accessed memory and registers
15    # with symbolic variables.
16    init_state = project.factory.blank_state(
17        addr=start_addr,
18        add_options = {
19            angr.options.SYMBOL_FILL_UNCONSTRAINED_MEMORY,
20            angr.options.SYMBOL_FILL_UNCONSTRAINED_REGISTERS
21        }
22    )
23
24    # From the disassembly we know that the check_password argument
25    # is fetched from the eax register, so we set it to a random memory
26    # address that is not used for anything else
27    init_state.regs.eax = pass_addr
28
29    # We create our simulation engine based on our initial state
30    simulation = project.factory.simgr(init_state)
31    # and tell it to explore states until it finds the good_addr and
32    # avoids the bad_addr
33    simulation.explore(find=good_addr, avoid=bad_addr)
34
35    # the found property is an array with states that reached our good_addr.
36    # If this exists, there's at least one solution. In this case there will only
37    # be one, there's only one way to reach the good_addr)
38    if simulation.found:
39        solution_state = simulation.found[0]
40        # We were using pass_addr as the source for the password, this will be
41        # filled with symbolic bit vectors that we must evaluate. Doing so will solve
42        # the constraints that exist and return a concrete value (which we cast to bytes
43        # and print as hex)
44        print(solution_state.solver.eval(solution_state.memory.load(pass_addr, 20), cast_to=bytes).hex())
45
46if __name__ == '__main__':
47    main()

If we run this, we’ll be disappointed to see it’s output:

~/pwnable.kr/collision$ python angr_solve.py 
ec09dd2100000000000000000000000000000000

Basically angr found the most obvious solution, to send the first chunk as the hashcode and all others as 0, but this is a problem for us, because we cannot send null bytes in the arguments.

To solve this we need to set constraints on the symbolic variables that represent the memory. We’ll do this by creating an array of 20 BVS, each with 8 bits in size, and adding constraints for each individual BVS:

 1... (added after line 23)
 2    # We create our BVS array of size 20, each BVS is a byte (BVS is in bits)
 3    password_chars = [claripy.BVS(f'password{i}', 8) for i in range(20)]
 4    # We create a final password which just concatenates all BVS, just to make it easier
 5    # to work with
 6    password = claripy.Concat(*password_chars)
 7
 8    # Here we define our constraints for each BVS. We are forcing the BVS values to
 9    # be in the printable ASCII.
10    for p in password_chars:
11        init_state.solver.add(p >= 0x20)
12        init_state.solver.add(p <= 0x7A)
13    # We store in our randomly chosen memory the password BVS array
14    init_state.memory.store(pass_addr, password, 20)
15
16    # From the disassembly we know that the check_password argument
17    # is fetched from the eax register, so we set it to a random memory
18    # address that is not used for anything else
19    init_state.regs.eax = pass_addr
20
21...
22        # We removed the .hex() as we have constraints to make the output printable ASCII
23        print(solution_state.solver.eval(solution_state.memory.load(pass_addr, 20), cast_to=bytes))
24...

If we now run this, we’ll get a valid string that will get us the flag. I won’t show the output to leave as an exercise for the reader. :)

Worth noting that on every run we get different outputs, because there’s a huge number of solutions (i.e. collisions) to this checksum. If we wanted to get multiple solutions instead of a single one, we could replace the solver.eval with solver.eval_upto and add a n=100 argument to get 100 solutions.

On a closing note, we can see the actual constraints by printing solution_state.solver.constraints:

[<Bool password0_5_8 >= 32>, <Bool password0_5_8 <= 122>, <Bool password1_6_8 >= 32>, <Bool password1_6_8 <= 122> ...repeats for all BVS...
<Bool (password3_8_8 .. password2_7_8 .. password1_6_8 .. password0_5_8) +
(password7_12_8 .. password6_11_8 .. password5_10_8 .. password4_9_8) +
(password11_16_8 .. password10_15_8 .. password9_14_8 .. password8_13_8) +
(password15_20_8 .. password14_19_8 .. password13_18_8 .. password12_17_8) +
(password19_24_8 .. password18_23_8 .. password17_22_8 .. password16_21_8) == 0x21dd09ec>]

The first line shows the constraints we manually added (to be ASCII), and on the remaining lines we see the constraint that forces the sum of the chunks to be equal to 0x21dd09ec, which were created by angr as the possible way to get into the branch we specified.

When we call solution_state.solver.eval we are interacting with Claripy. This is responsible for taking our constraints and using one of its backends to solve the SMT. In our case it will use z3 as the solver.

z3 method

This third method uses z3, which is an Satisfiability Modulo Theories (SMT) solver. When we used angr to symbolically run the program, it generated the constraints automatically after finding an AST that led into the branch that would run cat flag. Using z3, we must be the ones defining the constraints that will lead us to the output we want.

Let’s revisit the check_password function and it’s output validation so we can build our constraints based on it:

 1 unsigned long hashcode = 0x21DD09EC;
 2 unsigned long check_password(const char* p){
 3     int* ip = (int*)p;
 4     int i;
 5     int res=0;
 6     for(i=0; i<5; i++){
 7         res += ip[i];
 8     }
 9     return res;
10 }
11 int main(int argc, char* argv[]){
12 ...
13     if(hashcode == check_password( argv[1] )){
14         ...
15     }
16     else
17         ...
18     return 0;
19 }

Reiterating what we already described in the beginning, we must make the sum of a 5 int array (that we provide as 20B char) equal to 0x21DD09EC.

To z3 to solve this, again we must take into account some basics of it, which are very similar to angr:

• Concrete values are defined using BitVecVal
• Symbolic values are defined using BitVec
• We must create a Solver() object, where we add all our constraints
• We must check() if our constraints are solvable, this will either return sat or unsat
• If it’s sat, we take a model() from the solver, which represents a solution to our problem, and get the interpretation of the symbolic values into concrete values

Our z3 script will look like this:

 1from z3 import *
 2
 3def main():
 4    # Create our target value as a bit vector value
 5    target_sum = BitVecVal(0x21DD09EC, 32)
 6    
 7    # Create our password, which is a a list of 5 ints (32 bits)
 8    # We could also create a 20 byte array, but then we would have to create the
 9    # constraints differently
10    password = [BitVec(f'p_{i}', 32) for i in range(5)]
11
12    # The solver is where we add our constraints to
13    s = Solver()
14    # Our main constraint is that the sum of password ints must be equal to the target
15    s.add(Sum(password) == target_sum)
16
17    # Since we want ASCII only, we make a bitwise AND mask to extract the byte we want
18    # and make it between 0x20 and 0x7A. Another way to do it would be to shift right "p"
19    # and do the <= and >= check
20    for p in password:
21        s.add(0x20000000 <= p & 0xFF000000)
22        s.add(p & 0xFF000000 <= 0x7A000000)
23
24        s.add(0x00200000 <= p & 0x00FF0000)
25        s.add(p & 0x00FF0000 <= 0x007A0000)
26
27        s.add(0x00002000 <= p & 0x0000FF00)
28        s.add(p & 0x0000FF00 <= 0x00007A00)
29
30        s.add(0x00000020 <= p & 0x000000FF)
31        s.add(p & 0x000000FF <= 0x0000007A)
32
33    # check() validates that our model is satisfiable
34    # We make this a loop to get as many solutions as possible, or until we
35    # Ctrl+C
36    while s.check() == sat:
37        m = s.model()
38        out = b''
39        # After getting our model m, we iterate the password values,
40        # get the concrete values for each one with `m[p]`, convert it
41        # to bytes and concatenate to the `out`, which will have the password
42        for p in password:
43            out += m[p].as_long().to_bytes(4, byteorder='little')
44            # We also add a new constraint to discard this new value from future solutions,
45            # this way we get different outputs every time
46            s.add(p != m[p])
47        print(out)
48
49if __name__ == '__main__':
50    main()

Running this will keep printing strings that when summed will match our target value. Again, we’ll skip showing its output, and leave it as an exercise for the reader.

Conclusion

This was a rather lengthy post for such a simple challenge, but it was a good opportunity to show how symbolic execution and SMT solvers can be a very powerful tool when doing reversing and exploitation tasks.